

|
Optical Fiber Testing - The Math of Optical Loss
Optical Loss: Are You Positive It’s Positive?A post on a company’s blog and article on a magazine website discussed the topic of the polarity (meaning “+” or “-“ numbers) of measurements of optical loss, claiming loss was a positive number. The implication was that some people failed fourth grade math and did not understand positive and negative numbers. The claim is that insertion loss is always a positive number. Is that right?Well the real problem is that to understand this you need to understand logarithms and that’s Algebra II*, way beyond fourth grade addition and subtraction. You see dB is defined as a logarithmic function: 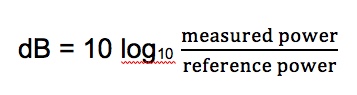 With logarithms, if the ratio of measured power to reference power is greater than 1, e.g. measured power is more than reference power, the log is positive. If the ratio of measured power to reference power is less than 1, e.g. measured power is less than reference power, the log is negative. If the ratio is 1, the log is 0. Since the logarithm for optical power ratio is base 10 and then multiplied by 10, each change of 10 in the ratio of the measured and reference power becomes a change of 10dB. E.g. +10 dB is a factor of 10 (10 times log10 10 which is 1), +20dB is a factor of 100 (10 times log10 100 which is 2), +30dB a factor of 1000 (10 times log10 1000 which is 3)and so on. Negative dB means division, so -10 dB means a factor of 1/10th (10 times log10 0.1 which is -1), -20dB a factor of 1/100th (10 times log10 0.01 which is -2) and so on. 0 dB means the measured power to reference power ratio is 1 – they are equal. Let’s try a graphic explanation of this equation. Take a look at this “semi-log” graph (logarithmic on the x axis and linear on the y axis) of dBm vs optical power in the range commonly used for fiber optics and calculated with our equation above. Remember 0 dBm means all power is referenced to 1 milliwatt optical power. 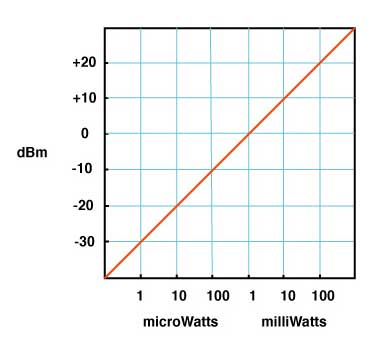 As you move to the right, power increases and the value in dBm gets more positive – that would be gain. So from 1mw to 10mw, we see a gain from 0dBm to +10dBm or 10dB, a positive change. As you move to the left, to lower optical power, as would be loss, the dBm value gets more negative. From 1mw to 100microwatts (that’s 1/10mw), we go from 0dBm to -10dBm, or -10dB; that negative change indicating a loss of 10dB. That shows gain is positive dB and loss is negative dB. Now we’re getting to the fourth grade math.* How about an example? Let’s say we decide to test a singlemode cable plant. We start with a laser source and launch cable which we measure our reference level for loss with a power meter to have an output of 0dBm. That’s 1 milliwatt of power, about the normal output of a fiber optic laser. After we attach the cable plant to test and a receive cable to our power meter, we measure 3dB loss. What power did we measure? The power must be lower, of course, since we have loss, and 3dB is approximately a factor of 2, so the power the meter measured is 1mw divided by 2 = 1/2milliwatt or 0.5mw. Since our power meter is measuring in dBm, it will read minus 3dBm (-3 dBm), since lower optical power is always more negative. If it read +3dBm, the power measured would be 2mw and that would be a gain from our reference (0dBm) which we know is incorrect – passive cable plants are not fiber amplifiers. Here is the graphical version of this loss test: 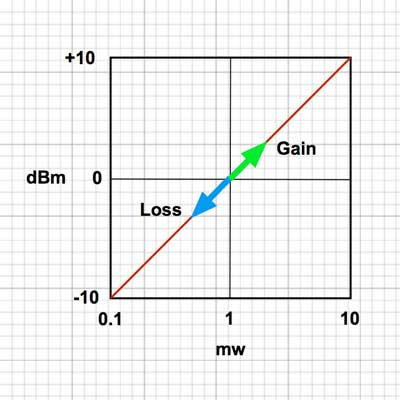 And then there is this short movie on the FOA Guide page explaining dB showing how a power meter shows loss when a cable is stressed to induce loss: 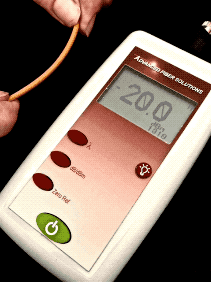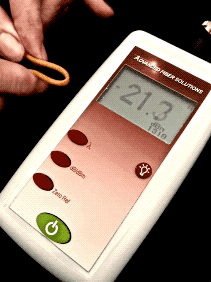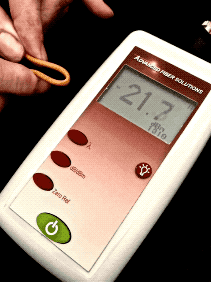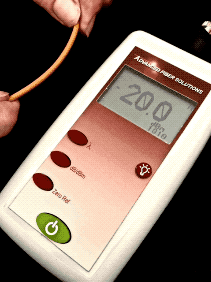 As the fiber is stressed, inducing loss, the power level goes from -20.0 dBm to --22.3 dBm.That's a more negative number. No question – loss means a more negative power reading in dB and a negative number in dB indicates loss.** But if you are a manufacturer of fiber optic test instruments that offers optical power meters and sources to test loss, why would this confuse you? Perhaps we should blame accounting. Suppose you have a company that has $1million in sales and $900,000 in expenses. What’s the profit? It’s $1,000,000 - $900,000 = $100,000. That’s a profit, right? But suppose your company has $1million in sales and $1,100,000 in expenses. What’s the bottom line? It’s $1,000,000 - $1,100,000 = - $100,000. Wait a minute, that is a negative number – that’s not a profit, it’s a loss. So in accounting, profits are positive numbers and losses are negative numbers when we do the math, but when we talk about loss, we don’t say we have a loss of “-$100,000,” we just have we have a loss of $100,000. Then we’ll put that number in parentheses when we publish our P&L like this ($100,000) and hope it doesn’t get noticed by investors, but you know it will. Loss and gain in fiber optic measurements are similar. If you are using a separate source and power meter, loss will be a negative number and gain will be a positive number. But because of convention, we sometimes drop the signs when we report the values because loss always means the optical power measurement was negative and gain means the optical power measurement was positive. But maybe that’s not what the convention has evolved to. Optical loss test sets (OLTS) aren’t designed to measure and display optical power, just loss. The actual power measured is lost in the algorithms used for calculating loss based on the “0dB” reference power and the measured loss. Long ago, most OLTS measured loss and displayed it as a negative number, but some companies who got into the fiber optic test equipment business from other test businesses arbitrarily decided to display loss as a positive number, and today most OLTS do show loss as a positive number. But when the instrument sees a gain, which it can do if improperly used, it therefore displays a negative number, which can be very confusing to a trained fiber tech who understands fiber optic power and loss measurements. OTDRs do the same thing. I looked at traces from a half-dozen OTDRs and all showed loss as a positive number and gain as a negative number. And yes, when you have a gainer in one direction, they show it as a negative number. Telling them that is wrong will fall on deaf ears, I’m afraid. The same article/blog post goes on to discuss optical return loss and reflectance, which has similar issues but they get it more or less right, which is confusing. Why can they understand that more negative numbers for reflectance means lower power in the reflectance but claim the opposite for insertion loss? The “less right” is that with most OTDRs reflectance of an event and optical return loss (ORL) are not the same thing. ORL is the summation of all reflectance events and fiber backscatter from the entire length of fiber. And, please, please stop saying “back reflection;” a reflection always goes back toward the source so the term is redundant and was dropped from fiber optics years ago. *So the problem is not simply fourth grade math, it also involves a bit of convention and tradition and marketing. And it requires understanding logarithms that create the negative number of loss. That’s more like Algebra II or 7th grade math, and here is a good tutorial from Kahn Academy on that: https://www.khanacademy.org/math/algebra2/exponential-and-logarithmic-functions/introduction-to-logarithms/v/logarithms And more basic, here is a tutorial on adding and subtracting negative numbers https://www.khanacademy.org/math/cc-seventh-grade-math ** If you want to calculate this yourself, FOA has a XLS spreadsheet you can download that will calculate the equations for optical power for you. The FOA has an explanation of dB on our online Guide and a couple of graphics that illustrate what happens with loss. More Power Meter MathAn industry contact recently sent us this question:I’ve been reading some of your articles relating to optical power meters, I’m struggling a bit with the maths relating to dBm. For example, if I apply -20dBm to an OPM and it’s accuracy spec is +/- 5%, then I would expect it to read between -21dBm and -19dBm. Similarly if the spec was +/-0.5dB then I would expect it to read between -19.5dBm and -20.5dBm. I’m not sure that is correct though, because dBm is logarithmic, I’m not sure you can add/subtract 5% or 0.5dB to it. Is there a way to work this out correctly ? Another one I’m struggling a bit with is linearity. Often the OPM manufacturer will express linearity as +/- 0.2dB. To me that means that if -20dBm is applied, and the OPM reads -19.8dBm then at -30dBm it should read -29.8 +/- 0.2dB (not -30dBm +/-0.2dB). One thing I’ve read about is least squares linear regression. I’m not entirely sure about this. FOA Response: It seems that this is an industry that is “math challenged,” especially when it comes to logarithms, with a top company writing articles saying that loss is a positive dB when it’s mathematically negative, and OTDR manufacturers all - ALL - have loss as a positive number. What drives us crazy is they also have gainers as negative numbers. See the section above. Lets look at some examples: +/-5% of 20dB can be interpreted as +/-1dB. But 20dB represents a multiplier of 100 so +/-5% could also mean +/-5% of 100 or 95 to 105. That turns out to be 19.78 dB ti 20.21dB or about +/-0.2dB. However 19dB = 79.4 and 21dB = 125.9 or about 25%. It can get even worse at other dB levels. At 30dB, +/-5 is 28.5 to 31.5 or a factor of 707 to 1412, almost a factor of two! That's understandable since +/-1.5dB is a range of 3dB which is a factor of two! I have seen many articles, even a few standards, that would say that a spec of +/-5% applied to dB would be +/-0.5dB at 10dB, +/-1dB at 20dB, etc. But of course that’s bad math; 0.5dB = ~12% and 1dB=~25%. Of course 5% in power difference is ~0.2dB and that holds no matter what the power level. FOA created a simple spreadsheet that calculates dB and linear power which allows you to play with numbers yourself and see the results. When it comes to linearity, the same applies. I believe that most will say a linearity of +/-0.2dB means about +/-5% and so 20dB is going to be 20dB+/-0.2dB, 30dB is going to be 30dB+/-0.2dB, etc. or actually ~5%. See the section on linearity toward the end of this page on optical power. There are several pages in the FOA Guide referenced above that cover this topic and this very technical one from an FOA instructor with a degree from MIT. |
|
|